



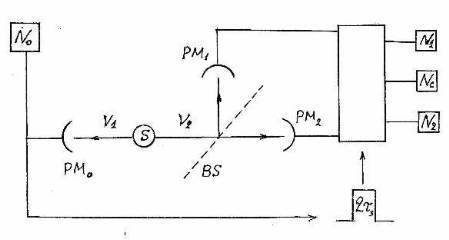
Fig.1. The scheme of installation of Grangier with co-autors. The signal of detector PM0 from the first photon ν1 opens an electronic gate for the time τ during which photomultipliers PM1 and PM2 are ready to accept the second photon ν2. S – radiation source, N1 – counter of the reflected photons, N2 – counter of the passed photons, Nc – coincidence counter of PM1 and PM2
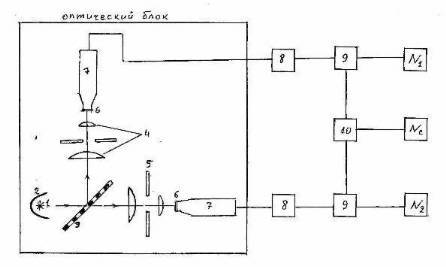
Fig. 2. The flowchart of our experimental installation. 1) light source; 2) parabolic reflector; 3) semitransparent mirror; 4) focusing lenses; 5) iris diaphragms; 6) working zones of photo-cathodes; 7) photomultipliers; 8) amplifiers of impulses; 9) threshold device – comparator; 10) high-speed logic scheme of coincidence; N1 – the counter of channel I; N2 – the counter of channel II; Nc – the coincidence counter.
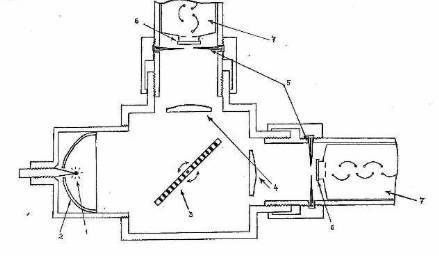
Fig.3
Fig. 4
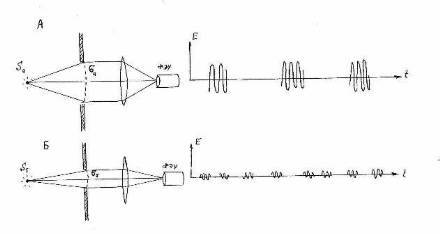
Fig. 5. Two possible situations at which PM register the same intensity. If light consists of photons these two situations are physically identical; if light consists of wave trains these situations are physically different.
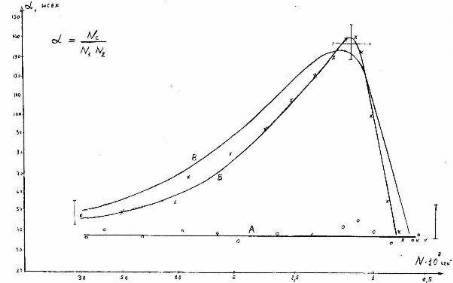
Fig. 6. A typical view of experimental dependences: A – the radiation stream is weakened by diaphragms 20 times;B – diaphragms are completely open; C– the theoretical curve. On the abscissa axis – rate of the count on the channels, decreasing with phosphor de-excitation; on the ordinate axis – the ratio α = Nc/N˛ (Nc – coincidence counting rate). Experimental curves are received with values T = 38 nsec; Nf1 = 700/sec; Nf2 = 500/sec (average values of measurements before experience). The theoretical curve is calculated for ND1 = ND2 = 600/sec; integral parameter of efficiency Р=2,2х10(-4)
PHOTONS OR WAVE TRAINS? DECISIVE EXPERIMENT. SCIENCE-POPULAR ARTICLE.
What is Light – Particles or Waves? New Experimental Data.
L.L.Regelson, A.A.Berezin, B.A.Kornilov. 1986
The article has been offered to popular scientific magazine "Science and Life" in the end of 1986, but has not been accepted. Here it is published with some additions which are not changing the sense of text (Lev Regelson). Acquainting the readers of magazine "the Science and the Life" with results of the experiment which did not still get all-round scientific approbation, we wish to invite the reader to participation in the process of the thrilling scientific search the final result of which is known still to nobody...
The problems of quantum theory became an integral part of our culture. Such concepts as quantum and a photon are familiar to everyone, many know about a paradoxical combination in one object of corpuscular and wave properties. It was connected with a big human drama of pioneers, creators of modern physics. Hard conservatism of the great scientific revolutionary Max Planck, Albert Einstein's grandiose polemic with Niels Bohr, intellectual tragedy of Ervin Shroedinger, painful hesitations of Louis De-Broglie, desperate resolution of Niels Bohr to reconsider all paradigm of scientific thought: who from thinking people of our time did not touch this bright and exciting history of formation of quantum picture of the world!
However the intellectual battle round these problems has not yet ended. In this year [1986] we became witnesses of outstanding scientific event: French physicists Grangier, Roger and Aspect have made the "key experiment" to give the direct answer to the question – does the light consist of wave trains or of particles – photons? [Europhys. Lett. V.1, 137-139, 1986].
The idea of their experiment: the radiation fell on semitransparent mirror which divided it in two equal parts, each part was registered by its own detector (PM). If light consists of photons such particle can or pass through a mirror, or be reflected by it. Under no circumstances the photon cannot get on both PM at once. It is absolutely true for a photon. However if there are not any photons, but only wave trains exist? In this case each train will be divided by mirror on two equal parts which will get on both detectors simultaneously. How it is possible to find out, what occurs actually?
Very simply – by directing of PM pulses to the counter pulse coincidence and to look, whether simultaneous operations of both detectors will take place. If light consists of photons, such coincidences are absolutely excluded. Quite another thing – the wave train: coincidences should be frequent enough.
But possibility should be excluded, that coincidence is caused by two different photons which have reached the mirror simultaneously. In this case one photon can go to one side, second photon – in another, and we receive coincidence which proves nothing. How to make, that only one photon was falling on a mirror each time, or, expressing on "quantum" language how to create "the one-photon state"?
The French scientists have found the witty decision. They used cascade character of radiation of atom: two photons with different frequencies ν1 and ν2 are emitted, during time τs. The first of these photons is used as "triggering", the second – as "operating" (see the experiment scheme on fig. 1). The excitation of atoms of calcium was performed by two lasers with the frequencies corresponding to two steps of transition.
The starting photon causes an impulse on detector PM0,and this impulse on a time
τ = 2τs switches on two other detectors: PM1 – for the photon which has passed through mirror BS and PM2 – for a photon reflected from mirror. Thus two "operating" photons cannot simultaneously reach the mirror. So that detectors could distinguish "starting" and "operating" photon, before PM0 the filter was put transparent only for frequency ν1, and before PM1 and PM2 – the filters only for frequency ν2.
Now, at last, it is possible with pure conscience to count the coincidences of PM1 and PM2 to find out, the light consists of photons or of wave trains. Result of experiment of the French scientists: excess of number of coincidences over the noises is not observed.
It means – light consists of photons!
But Grangier with co-authors did not restrict themselves with this experiment. Using their method of receiving of single photons, they have replaced photomultipliers PM1 and PM2 with entrance windows of interferometer. And the interference picture was accurately observed! So, the photon was single, and had interference with itself!
Thus, the paradox of wave-corpuscle dualism was proved once again, more convincingly than before. And the conception of Niels Bohr remains the only solution: the real wave does not exist, there is only photon, but probability of its detection in this or that place is defined by wave equation.
It seems, this time the question is solved definitively and irrevocably!
But nevertheless we shall dare to doubt it.
When we have made similar experiment, we did not know about result of Frenchmen: our messages were published practically simultaneously. But our experiment has yielded results which conduct to an opposite conclusion: light consists from wave trains, and no photons exist!
Here is the block diagram of our experiment (Fig. 2).
Our experiment differs from French variant: we had no possibility to create "single-photon state". How is it possible to guarantee – irrespective of, light consists of photons or trains – that they are not imposed accidentally one on other? We may be confident that each photon (train) is counted separately only because the average interval of time between following photons (trains) was much more than time resolution of detection system.
For those whom technical details interest, we show "interior" of the optical block (a Fig. 3):
Here it is "in metal" (Fig. 4).
The idea of experiment: the account rate of coincidence will be different for a stream of photons and for sequence of wave trains.
Let's deduce the formulas to calculate this rate for each of these cases.
I. Light is the stream of photons
We designate as NF the number of the photons which are emitted by a source per second, and as N1 and N2 – rates of counts; we will suppose N1 = N2 = N. Then the total rate of count is equal N1 + N2 = 2N. Let's introduce the integral parameter of photon counting efficiency:
Р = 2 NL/NF or NL = РNF /2 (1)
Here NL – number of counts on the detector, caused only by light, instead of other reasons (external disturbances and internal noises). Р is equal to the number of detectors pulse counts which will take place on one photon which has been emitted by the source.
Except "light impulses" it is necessary to take into consideration also "dark impulses", caused by the cathode, which emits some number of electrons without any lighting. To appear an impulse on outlet of PM, one thing is necessary only: emission by the photocathode a primary electron – for what reason it has appeared, PM does not distinguish.
Thus, the detector always counts only the sum of light and dark impulses:
N = NL + ND
where ND – rate of counting of dark impulses.
Taking into account (1) it is possible to write:
Р = 2 (N – ND)/NF
N = (Р NF/2) + ND
NF = 2 (N – ND)/P (2)
Now we will introduce one more important parameter. Each of detectors has the resolving time Т which defines, which time interval should separate from each other two consecutive photons so that the detector could give a separate signal for each of them. If the interval between photons is less than Т, both signals would merge in one.
As speed of the count of PM pulses (with the account of dark pulses) is equal N, the probability of appearing of impulse on one of detectors during Т is equal:
P1 = Т [(РNF/2) + ND] = NТ (3)
The probability of appearing an impulse on other detector in the same interval Т, also is equal:
P2 = NТ
As the photon can reach only one of two detectors, but not both at once occurrences of impulses on each of PM are independent events. Such events coincidence probability, i.e. probability of occurrence of signals on two detectors at once during the same interval of time Т, is equal to product of probabilities, i.e.:
P12 = P1P2 = (NТ)(2)
To receive the coincidence counting rate Nс, i.e. the number of coincidences in the unit of time, it is necessary to divide this probability on Т. Taking into account (2) we receive:
Nс = P/T = (NТ)(2))/T = TN(2) (4)
This is the formula of coincidence for photons. The only condition of its applicability: photons should not be emitted by groups. Such situation can arise, if emission acts of separate atoms are not independent events, but have influence against each other. One of the photons entering into such compact cluster, can pass through a semitransparent mirror, and another – be reflected from it, and detectors will have operated simultaneously.
Then in the formula (4) there will be the additional member expressing degree of grouping of photons. Such situation really arises, for example, in astronomical measurements of statistics of the photons from star sources of light. In gaseous and plasma sources there are pulsations of radiation which lead to effect of grouping of photons. Thus the number of photo-count coincidences on two detectors exceeds the number of accidental coincidences defined by the formula (3). Excess is insignificant, but it has the statistical confidence, and this phenomenon is successfully used for receiving more information about character of radiation of star sources.
II. Light is the aggregate of wave trains.
All reasoning having used in derivation of the formula (3), are applicable also for calculation of accidental imposition of one train on another during T. But in the case of trains there should appear the additional coincidences:
Nс = TN(2) + Nсt (5)
where quantity Nсt shows the coincidences specific only for trains, and not having place for photons. Expression for an estimation of this quantity we now should deduce.
The average number of impulses on the detector to one wave train is similar to expression (1) for photons, with replacement NF (number of photons) on Nt (number of trains):
N = (РNt/2) + ND = Nt + ND (6)
But further we meet something unexpectedness!
Let's reason consistently. When wave train had fallen on a photocathode surface, in any point of its front the photoelectron can be knocked out. If in some point the act of knocking-out had already occurred, in other points of wave the situation has not changed. "Reduction of wave packet" in this case cannot be – it is the train of the real wave!
It means, after electron knocking-out in one point of the photocathode the probability of another electron knocking-out in other point remains the same. An amazing conclusion: there is probability that one train will cause appearing at once two and more photoelectrons on one cathode.
As appearances of photoelectrons in different points of train are independent events, the probability of appearance n photoelectrons (and accordingly – impulses of PM) from one train on one cathode is defined by Poisson distribution:
P(n) = a(2) [exp(-a)]/n!
Here a – average value of photo-count number by one train of one detector.
Inasmuch as on the detector only a half of train comes, so according to definition of efficiency Р(1):
a = Р/2
Substituting this value in Poisson formula onto values n = 0,1,2… we will receive for the first detector:
P1(0) = exp (-R/2) ≈ 1 (as Р <<1)
P1(1) ≈ Р/2
P1(2) ≈ (Р/2)(2)/2
Here P1(0) – probability that train will cause appearance of no impulse; P1(2) – probability that train will cause appearance of two impulses.
Similarly for the second detector:
P2(0) ≈ 1
P2(1) ≈ Р/2
P2(2) ≈ (Р/2)(2)/2
Now we will define, what probability of what the signal will appear simultaneously on the first and second detector? Inasmuch as PM impulse produced by two and more electrons on the cathode, will be counted as one signal we receive probabilities for different variants of coincidence:
P1(1) P2(1) = (Р/2)(2)
P1(1) P2 (2) + P1(2) P2 (1) = 2 (Р/2)
(Р/2)(2)/2 = Р(3)/4
As the probability of the second combination is much less than the first it is possible to estimate probability of coincidence of signals on two detectors as:
P12 = (Р/2)(2)
As the number of trains per unit of time is Nt, we receive for Nсt in (5), taking into account (2):
Nсt = P12Nt = (Р/2)(2)Nt = (Р/2)(2) 2(N – ND)/P
Nсt = Р(N – ND)/2 (7)
The coincidences rate which is observed, is defined according to (5), by the sum:
Nс = TN(2) + Nсt = TN(2) + P(N – ND)/2 (8)
For an estimation of results of experiment we will introduce the parameter of correlation:
α(N) = Nс /N(2) = T + P(N – ND)/2N(2) (9)
From here it is obvious, that to the observation of super-correlation effect caused by splitting of wave train, it is necessary, that the second member in these formulas was not too small in comparison with the unit, i.e. the ratio:
P(N – ND)/2N(2)T ≈ P/2NT (10)
should not be small in comparison with 1.
Thus, the experiment could answer to the question: waves or particles – only by fulfillment of three conditions:
1. Source radiation should be stochastic;
2. Intensity of radiation should be small enough (8);
3. Integral efficiency is not too small (10).
To satisfy first two conditions, we have chosen as a source the long-living crystal phosphor with the radiating centres concluded in deep potential wells (ZnS, doping by Co). On a measure of de-excitation of phosphor the intensity becomes small, and stochasticity is guaranteed by absence of interaction between the "cobalt traps" separated by a high potential barrier from a lattice of a crystal.
Parameter Р means total count number on two channels per one act of emission in atom of a source. P depends on quality of focusing, losses of light in optics, the sizes of apertures of diaphragms, quantum efficiency of PM and losses of impulses in electronics. The requirement of not too small value Р makes, so to say, the "highlight" of our experiment. Numerous experiments with photons statistics could not discover the effect of "train splitting" because inevitable using of diaphragms with small apertures made this effect too small in comparison with accidental coincidence (the first member of the formula 8). The value of Р ≈ 0,2х10(-3) has been reached in our experiment. It not too little: one who wishes to repeat this experiment may try to receive more. He should first of all replace PM with their quantum efficiency no more than 5%, on charge-coupled device with efficiency 10 times more. Unfortunately, we had not such detectors on hand.
There was such sequence of actions in our experiment. With completely closed diaphragms (to avoid the "blinding" of photo-cathodes) the source was taken out, lighted by 100-watt incandescent lamp during 2-3 sec and then inserted on its place. Diaphragms had been completely opened and optics adjustment has made to provide maximum and equal values of count rate on each channel. Then the light streams were limited by diaphragms so that indications of each counter have decreased at 20-50 time, remaining equal each other. During de-excitation of phosphor the indications on counters of channels and the counter of coincidence were registered until the counting number on channels has fallen to 400-500/sec that corresponded to light reduced about 20 times.
After that diaphragms had been completely opened and registration of the "working" series began which correspond to the maximum of value α(N). The reading out of count rates continued until the number of light impulses became small in comparison with number of dark impulses. I.e. full count rate on channels became nearer to rate of dark impulses, which was defined by preliminary measurements. After that the diaphragms were closed and dark impulses rate was again measured.
Thus, we could compare dependence of coincidence number with count number on channels for various degree of diaphragms disclosing. Saying otherwise we had possibility to compare correlation properties of two electromagnetic fields, equal on intensity but differing on degree of dissociation of single wave trains (Fig. 5).
Dependence of correlation parameter α on intensity of radiation was studied, more precisely, on impulses count rate on each channel. Theoretical expression for α(N) is set by formula (9). It is not hard to be convinced, that the maximum of this function is reached at
N* = 2ND (11)
where N* – number of "light" pulses is equal to number of dark pulses, and value of this maximum is:
α* = T + P/4ND (12)
Results of our experiment completely confirm the validity of expressions (11) and (12). The typical result is presented on the graph (Fig.6) where values of N are given in a logarithmic scale. At high intensity (N about 30.000/sec and more) the value α was near to resolving time T = 38 nsec. As accidental impositions of independent acts of emission here prevail it is possible to name this value "stochastic". If light would consist of photons this value should not vary up to full fading of luminescence when only dark impulses would be counted.
However the picture turns out absolutely another: the correlation parameter reaches a maximum at N = 2ND and value α in a maximum more than three times (!) exceeds what would take a place if light consisted of photons. At the further reduction of intensity the fraction of light impulses will fall, the parameter α again starts to be defined by accidental impositions of impulses (this time – dark pulses) and comes back to the "stochastic" value.
If our conclusions are true and the light consists from trains instead of photons, the new hard-soluble questions arise. Here is the main. The train in the emission act receives from atom the energy hν, and in some cases knocks out at once two photoelectrons, each of which receives the same energy hν – i.e. the train energy will be doubled. How to be with the law of energy conservation? Perhaps, Shroedinger was right when he asserted that energy is only statistical concept like temperature so this concept is unsuitable to individual events in a microworld?
The note of 1986. (Lev Regelson)
I consider now this problem does not exist. See addition in the end of article.
In conclusion we should answer other question: why results of Grangier experiment so radically differ from ours? Someone obviously, had mistaken. Taking into account the technical equipment and degree of scientific training of authors the natural conclusion arises namely we who made mistake. But we will not give up without fight and shall try to look, whether are not in experiment some "hidden reefs", which was not noticed by French scientists?
The main difference between our experiments: they had not put the reflector and the lenses collecting all "working" radiation at the windows of detectors. As a result each window "cuts out" only small part of falling wave front – it would correspond to variant B in Fig. 5. In these conditions they could not detect the coincidences, caused by the same wave train. Authors point out in the end of their article that for production of "single-photon states" they should collect all radiation within a solid angle 4π, but in their installation it was inconvenient to make it...
Thus, nothing is proved yet. We subject all this to great doubt. We have no right to trust ourselves: the history represents many examples of the most surprising subjective errors of experimenters. If it would be desirable to prove something, the search of "hidden reefs" becomes not very scrutinizing... In such cases the convincing evidence could be received only by independent repetitions of experiment in different variants, in various laboratories and the subsequent critical discussion of results by world scientific community. Our aim is only scientific truth: we will be grateful to those experimenters who will disprove our results. In this case the Copenhagen interpretation of the quantum theory subjected to verification from a new angle of view, will receive more strong foundation.
But if our results will be reliably confirmed, the great dispute about the bases of quantum picture of world would get into new phase...
Additions of 2009 (Lev Regelson).
1. To the question about nonconservation of energy in the individual interactions.
The seeming "paradox" arises from the incorrect assumption, as if the real wave train is always "normalized" to 1. In other words, it is supposed, that the integral from a square of the module of amplitude on all volume of train emitted by atom is always identical and can be set equal to 1. On the same erroneous assumption Bell theorem is based: if to cancel normalization of probabilities to 1, the proof of theorem has lost force. Only the stationary configurations of electronic shells of atoms are discrete and normalized. The modern quantum optics has accertained that an exchange of energy with an external field occurs without any jumps; the transition from one electron configuration to another and back occurs continuously according to the sinusoidal law. Thus, it may be emitted not inevitable the whole train, corresponding to full transition, but some small part of single-photon train, corresponding to small part of electron cloud which was at the upper level at the moment of emission.
2. In regard with results of experiment Grangier, Roger and Аspect.
More careful examination may show, that, despite a small solid angle of registration of radiation they still could observe super-correlations if one more factor has not played a main role: emission of the "incomplete" trains by atoms of calcium. Population of the upper state is defined by the square of relation of Rabi frequency to the deviation of external field frequency from strict resonance. Rabi frequency, in its turn, is proportional to amplitude of external field. As result the trains of small intensity had been emitted: it is equivalent to the situation B in Fig. 5 or to diminution of parameter Р in the formula (9). [See next articles on this site]. The same reason – incomplete filling of radiating states of phosphor – may explain too small value Р in our experience (Fig. 6). Nevertheless, unlike the French experiment, our value was sufficient for reliable observing of super-correlations.
reliable observing of super-correlations.
L.L.Regelson, A.A.Berezin, B.A.Kornilov. 1986
The article has been offered to popular scientific magazine "Science and Life" in the end of 1986, but has not been accepted. Here it is published with some additions which are not changing the sense of text (Lev Regelson). Acquainting the readers of magazine "the Science and the Life" with results of the experiment which did not still get all-round scientific approbation, we wish to invite the reader to participation in the process of the thrilling scientific search the final result of which is known still to nobody...
The problems of quantum theory became an integral part of our culture. Such concepts as quantum and a photon are familiar to everyone, many know about a paradoxical combination in one object of corpuscular and wave properties. It was connected with a big human drama of pioneers, creators of modern physics. Hard conservatism of the great scientific revolutionary Max Planck, Albert Einstein's grandiose polemic with Niels Bohr, intellectual tragedy of Ervin Shroedinger, painful hesitations of Louis De-Broglie, desperate resolution of Niels Bohr to reconsider all paradigm of scientific thought: who from thinking people of our time did not touch this bright and exciting history of formation of quantum picture of the world!
However the intellectual battle round these problems has not yet ended. In this year [1986] we became witnesses of outstanding scientific event: French physicists Grangier, Roger and Aspect have made the "key experiment" to give the direct answer to the question – does the light consist of wave trains or of particles – photons? [Europhys. Lett. V.1, 137-139, 1986].
The idea of their experiment: the radiation fell on semitransparent mirror which divided it in two equal parts, each part was registered by its own detector (PM). If light consists of photons such particle can or pass through a mirror, or be reflected by it. Under no circumstances the photon cannot get on both PM at once. It is absolutely true for a photon. However if there are not any photons, but only wave trains exist? In this case each train will be divided by mirror on two equal parts which will get on both detectors simultaneously. How it is possible to find out, what occurs actually?
Very simply – by directing of PM pulses to the counter pulse coincidence and to look, whether simultaneous operations of both detectors will take place. If light consists of photons, such coincidences are absolutely excluded. Quite another thing – the wave train: coincidences should be frequent enough.
But possibility should be excluded, that coincidence is caused by two different photons which have reached the mirror simultaneously. In this case one photon can go to one side, second photon – in another, and we receive coincidence which proves nothing. How to make, that only one photon was falling on a mirror each time, or, expressing on "quantum" language how to create "the one-photon state"?
The French scientists have found the witty decision. They used cascade character of radiation of atom: two photons with different frequencies ν1 and ν2 are emitted, during time τs. The first of these photons is used as "triggering", the second – as "operating" (see the experiment scheme on fig. 1). The excitation of atoms of calcium was performed by two lasers with the frequencies corresponding to two steps of transition.
The starting photon causes an impulse on detector PM0,and this impulse on a time
τ = 2τs switches on two other detectors: PM1 – for the photon which has passed through mirror BS and PM2 – for a photon reflected from mirror. Thus two "operating" photons cannot simultaneously reach the mirror. So that detectors could distinguish "starting" and "operating" photon, before PM0 the filter was put transparent only for frequency ν1, and before PM1 and PM2 – the filters only for frequency ν2.
Now, at last, it is possible with pure conscience to count the coincidences of PM1 and PM2 to find out, the light consists of photons or of wave trains. Result of experiment of the French scientists: excess of number of coincidences over the noises is not observed.
It means – light consists of photons!
But Grangier with co-authors did not restrict themselves with this experiment. Using their method of receiving of single photons, they have replaced photomultipliers PM1 and PM2 with entrance windows of interferometer. And the interference picture was accurately observed! So, the photon was single, and had interference with itself!
Thus, the paradox of wave-corpuscle dualism was proved once again, more convincingly than before. And the conception of Niels Bohr remains the only solution: the real wave does not exist, there is only photon, but probability of its detection in this or that place is defined by wave equation.
It seems, this time the question is solved definitively and irrevocably!
But nevertheless we shall dare to doubt it.
When we have made similar experiment, we did not know about result of Frenchmen: our messages were published practically simultaneously. But our experiment has yielded results which conduct to an opposite conclusion: light consists from wave trains, and no photons exist!
Here is the block diagram of our experiment (Fig. 2).
Our experiment differs from French variant: we had no possibility to create "single-photon state". How is it possible to guarantee – irrespective of, light consists of photons or trains – that they are not imposed accidentally one on other? We may be confident that each photon (train) is counted separately only because the average interval of time between following photons (trains) was much more than time resolution of detection system.
For those whom technical details interest, we show "interior" of the optical block (a Fig. 3):
Here it is "in metal" (Fig. 4).
The idea of experiment: the account rate of coincidence will be different for a stream of photons and for sequence of wave trains.
Let's deduce the formulas to calculate this rate for each of these cases.
I. Light is the stream of photons
We designate as NF the number of the photons which are emitted by a source per second, and as N1 and N2 – rates of counts; we will suppose N1 = N2 = N. Then the total rate of count is equal N1 + N2 = 2N. Let's introduce the integral parameter of photon counting efficiency:
Р = 2 NL/NF or NL = РNF /2 (1)
Here NL – number of counts on the detector, caused only by light, instead of other reasons (external disturbances and internal noises). Р is equal to the number of detectors pulse counts which will take place on one photon which has been emitted by the source.
Except "light impulses" it is necessary to take into consideration also "dark impulses", caused by the cathode, which emits some number of electrons without any lighting. To appear an impulse on outlet of PM, one thing is necessary only: emission by the photocathode a primary electron – for what reason it has appeared, PM does not distinguish.
Thus, the detector always counts only the sum of light and dark impulses:
N = NL + ND
where ND – rate of counting of dark impulses.
Taking into account (1) it is possible to write:
Р = 2 (N – ND)/NF
N = (Р NF/2) + ND
NF = 2 (N – ND)/P (2)
Now we will introduce one more important parameter. Each of detectors has the resolving time Т which defines, which time interval should separate from each other two consecutive photons so that the detector could give a separate signal for each of them. If the interval between photons is less than Т, both signals would merge in one.
As speed of the count of PM pulses (with the account of dark pulses) is equal N, the probability of appearing of impulse on one of detectors during Т is equal:
P1 = Т [(РNF/2) + ND] = NТ (3)
The probability of appearing an impulse on other detector in the same interval Т, also is equal:
P2 = NТ
As the photon can reach only one of two detectors, but not both at once occurrences of impulses on each of PM are independent events. Such events coincidence probability, i.e. probability of occurrence of signals on two detectors at once during the same interval of time Т, is equal to product of probabilities, i.e.:
P12 = P1P2 = (NТ)(2)
To receive the coincidence counting rate Nс, i.e. the number of coincidences in the unit of time, it is necessary to divide this probability on Т. Taking into account (2) we receive:
Nс = P/T = (NТ)(2))/T = TN(2) (4)
This is the formula of coincidence for photons. The only condition of its applicability: photons should not be emitted by groups. Such situation can arise, if emission acts of separate atoms are not independent events, but have influence against each other. One of the photons entering into such compact cluster, can pass through a semitransparent mirror, and another – be reflected from it, and detectors will have operated simultaneously.
Then in the formula (4) there will be the additional member expressing degree of grouping of photons. Such situation really arises, for example, in astronomical measurements of statistics of the photons from star sources of light. In gaseous and plasma sources there are pulsations of radiation which lead to effect of grouping of photons. Thus the number of photo-count coincidences on two detectors exceeds the number of accidental coincidences defined by the formula (3). Excess is insignificant, but it has the statistical confidence, and this phenomenon is successfully used for receiving more information about character of radiation of star sources.
II. Light is the aggregate of wave trains.
All reasoning having used in derivation of the formula (3), are applicable also for calculation of accidental imposition of one train on another during T. But in the case of trains there should appear the additional coincidences:
Nс = TN(2) + Nсt (5)
where quantity Nсt shows the coincidences specific only for trains, and not having place for photons. Expression for an estimation of this quantity we now should deduce.
The average number of impulses on the detector to one wave train is similar to expression (1) for photons, with replacement NF (number of photons) on Nt (number of trains):
N = (РNt/2) + ND = Nt + ND (6)
But further we meet something unexpectedness!
Let's reason consistently. When wave train had fallen on a photocathode surface, in any point of its front the photoelectron can be knocked out. If in some point the act of knocking-out had already occurred, in other points of wave the situation has not changed. "Reduction of wave packet" in this case cannot be – it is the train of the real wave!
It means, after electron knocking-out in one point of the photocathode the probability of another electron knocking-out in other point remains the same. An amazing conclusion: there is probability that one train will cause appearing at once two and more photoelectrons on one cathode.
As appearances of photoelectrons in different points of train are independent events, the probability of appearance n photoelectrons (and accordingly – impulses of PM) from one train on one cathode is defined by Poisson distribution:
P(n) = a(2) [exp(-a)]/n!
Here a – average value of photo-count number by one train of one detector.
Inasmuch as on the detector only a half of train comes, so according to definition of efficiency Р(1):
a = Р/2
Substituting this value in Poisson formula onto values n = 0,1,2… we will receive for the first detector:
P1(0) = exp (-R/2) ≈ 1 (as Р <<1)
P1(1) ≈ Р/2
P1(2) ≈ (Р/2)(2)/2
Here P1(0) – probability that train will cause appearance of no impulse; P1(2) – probability that train will cause appearance of two impulses.
Similarly for the second detector:
P2(0) ≈ 1
P2(1) ≈ Р/2
P2(2) ≈ (Р/2)(2)/2
Now we will define, what probability of what the signal will appear simultaneously on the first and second detector? Inasmuch as PM impulse produced by two and more electrons on the cathode, will be counted as one signal we receive probabilities for different variants of coincidence:
P1(1) P2(1) = (Р/2)(2)
P1(1) P2 (2) + P1(2) P2 (1) = 2 (Р/2)
(Р/2)(2)/2 = Р(3)/4
As the probability of the second combination is much less than the first it is possible to estimate probability of coincidence of signals on two detectors as:
P12 = (Р/2)(2)
As the number of trains per unit of time is Nt, we receive for Nсt in (5), taking into account (2):
Nсt = P12Nt = (Р/2)(2)Nt = (Р/2)(2) 2(N – ND)/P
Nсt = Р(N – ND)/2 (7)
The coincidences rate which is observed, is defined according to (5), by the sum:
Nс = TN(2) + Nсt = TN(2) + P(N – ND)/2 (8)
For an estimation of results of experiment we will introduce the parameter of correlation:
α(N) = Nс /N(2) = T + P(N – ND)/2N(2) (9)
From here it is obvious, that to the observation of super-correlation effect caused by splitting of wave train, it is necessary, that the second member in these formulas was not too small in comparison with the unit, i.e. the ratio:
P(N – ND)/2N(2)T ≈ P/2NT (10)
should not be small in comparison with 1.
Thus, the experiment could answer to the question: waves or particles – only by fulfillment of three conditions:
1. Source radiation should be stochastic;
2. Intensity of radiation should be small enough (8);
3. Integral efficiency is not too small (10).
To satisfy first two conditions, we have chosen as a source the long-living crystal phosphor with the radiating centres concluded in deep potential wells (ZnS, doping by Co). On a measure of de-excitation of phosphor the intensity becomes small, and stochasticity is guaranteed by absence of interaction between the "cobalt traps" separated by a high potential barrier from a lattice of a crystal.
Parameter Р means total count number on two channels per one act of emission in atom of a source. P depends on quality of focusing, losses of light in optics, the sizes of apertures of diaphragms, quantum efficiency of PM and losses of impulses in electronics. The requirement of not too small value Р makes, so to say, the "highlight" of our experiment. Numerous experiments with photons statistics could not discover the effect of "train splitting" because inevitable using of diaphragms with small apertures made this effect too small in comparison with accidental coincidence (the first member of the formula 8). The value of Р ≈ 0,2х10(-3) has been reached in our experiment. It not too little: one who wishes to repeat this experiment may try to receive more. He should first of all replace PM with their quantum efficiency no more than 5%, on charge-coupled device with efficiency 10 times more. Unfortunately, we had not such detectors on hand.
There was such sequence of actions in our experiment. With completely closed diaphragms (to avoid the "blinding" of photo-cathodes) the source was taken out, lighted by 100-watt incandescent lamp during 2-3 sec and then inserted on its place. Diaphragms had been completely opened and optics adjustment has made to provide maximum and equal values of count rate on each channel. Then the light streams were limited by diaphragms so that indications of each counter have decreased at 20-50 time, remaining equal each other. During de-excitation of phosphor the indications on counters of channels and the counter of coincidence were registered until the counting number on channels has fallen to 400-500/sec that corresponded to light reduced about 20 times.
After that diaphragms had been completely opened and registration of the "working" series began which correspond to the maximum of value α(N). The reading out of count rates continued until the number of light impulses became small in comparison with number of dark impulses. I.e. full count rate on channels became nearer to rate of dark impulses, which was defined by preliminary measurements. After that the diaphragms were closed and dark impulses rate was again measured.
Thus, we could compare dependence of coincidence number with count number on channels for various degree of diaphragms disclosing. Saying otherwise we had possibility to compare correlation properties of two electromagnetic fields, equal on intensity but differing on degree of dissociation of single wave trains (Fig. 5).
Dependence of correlation parameter α on intensity of radiation was studied, more precisely, on impulses count rate on each channel. Theoretical expression for α(N) is set by formula (9). It is not hard to be convinced, that the maximum of this function is reached at
N* = 2ND (11)
where N* – number of "light" pulses is equal to number of dark pulses, and value of this maximum is:
α* = T + P/4ND (12)
Results of our experiment completely confirm the validity of expressions (11) and (12). The typical result is presented on the graph (Fig.6) where values of N are given in a logarithmic scale. At high intensity (N about 30.000/sec and more) the value α was near to resolving time T = 38 nsec. As accidental impositions of independent acts of emission here prevail it is possible to name this value "stochastic". If light would consist of photons this value should not vary up to full fading of luminescence when only dark impulses would be counted.
However the picture turns out absolutely another: the correlation parameter reaches a maximum at N = 2ND and value α in a maximum more than three times (!) exceeds what would take a place if light consisted of photons. At the further reduction of intensity the fraction of light impulses will fall, the parameter α again starts to be defined by accidental impositions of impulses (this time – dark pulses) and comes back to the "stochastic" value.
If our conclusions are true and the light consists from trains instead of photons, the new hard-soluble questions arise. Here is the main. The train in the emission act receives from atom the energy hν, and in some cases knocks out at once two photoelectrons, each of which receives the same energy hν – i.e. the train energy will be doubled. How to be with the law of energy conservation? Perhaps, Shroedinger was right when he asserted that energy is only statistical concept like temperature so this concept is unsuitable to individual events in a microworld?
The note of 1986. (Lev Regelson)
I consider now this problem does not exist. See addition in the end of article.
In conclusion we should answer other question: why results of Grangier experiment so radically differ from ours? Someone obviously, had mistaken. Taking into account the technical equipment and degree of scientific training of authors the natural conclusion arises namely we who made mistake. But we will not give up without fight and shall try to look, whether are not in experiment some "hidden reefs", which was not noticed by French scientists?
The main difference between our experiments: they had not put the reflector and the lenses collecting all "working" radiation at the windows of detectors. As a result each window "cuts out" only small part of falling wave front – it would correspond to variant B in Fig. 5. In these conditions they could not detect the coincidences, caused by the same wave train. Authors point out in the end of their article that for production of "single-photon states" they should collect all radiation within a solid angle 4π, but in their installation it was inconvenient to make it...
Thus, nothing is proved yet. We subject all this to great doubt. We have no right to trust ourselves: the history represents many examples of the most surprising subjective errors of experimenters. If it would be desirable to prove something, the search of "hidden reefs" becomes not very scrutinizing... In such cases the convincing evidence could be received only by independent repetitions of experiment in different variants, in various laboratories and the subsequent critical discussion of results by world scientific community. Our aim is only scientific truth: we will be grateful to those experimenters who will disprove our results. In this case the Copenhagen interpretation of the quantum theory subjected to verification from a new angle of view, will receive more strong foundation.
But if our results will be reliably confirmed, the great dispute about the bases of quantum picture of world would get into new phase...
Additions of 2009 (Lev Regelson).
1. To the question about nonconservation of energy in the individual interactions.
The seeming "paradox" arises from the incorrect assumption, as if the real wave train is always "normalized" to 1. In other words, it is supposed, that the integral from a square of the module of amplitude on all volume of train emitted by atom is always identical and can be set equal to 1. On the same erroneous assumption Bell theorem is based: if to cancel normalization of probabilities to 1, the proof of theorem has lost force. Only the stationary configurations of electronic shells of atoms are discrete and normalized. The modern quantum optics has accertained that an exchange of energy with an external field occurs without any jumps; the transition from one electron configuration to another and back occurs continuously according to the sinusoidal law. Thus, it may be emitted not inevitable the whole train, corresponding to full transition, but some small part of single-photon train, corresponding to small part of electron cloud which was at the upper level at the moment of emission.
2. In regard with results of experiment Grangier, Roger and Аspect.
More careful examination may show, that, despite a small solid angle of registration of radiation they still could observe super-correlations if one more factor has not played a main role: emission of the "incomplete" trains by atoms of calcium. Population of the upper state is defined by the square of relation of Rabi frequency to the deviation of external field frequency from strict resonance. Rabi frequency, in its turn, is proportional to amplitude of external field. As result the trains of small intensity had been emitted: it is equivalent to the situation B in Fig. 5 or to diminution of parameter Р in the formula (9). [See next articles on this site]. The same reason – incomplete filling of radiating states of phosphor – may explain too small value Р in our experience (Fig. 6). Nevertheless, unlike the French experiment, our value was sufficient for
 reliable observing of super-correlations.
reliable observing of super-correlations. 